KAK – Tänään kesäkuun 21. päivänä on kesäpäivänseisaus (tarkka hetki oli kello 5.43.). Useimmille meistä se merkitsee juhannusta ja juhlimista monin tavoin. Jos omistat kesämökin tai huvilan, olet varmaankin siellä perheesi ja tai ystäviesi kanssa. Jos et omista mökkiä tai et jostakin syystä pääse matkustamana sinne, niin ehkä kotipaikkakunnallasi järjestettiin yhteisiä juhlia kokoineen aattoiltana. Tai jos viihdyt paremmin yksiksesi tai vaikka puolisosi kanssa, silloin uskoakseni olet kuitenkin juhlatuulella, onhan tämä vuoden parasta aikaan (vaikka joidenkin mielestä syksy tai talvi on parasta).
Kesäpäivänseisaus ei ole vain juhla, vaan sillä on myös astronominen
merkitys. Tässä artikkelissa käsittelen maapallon vuotta, sillä maapallon
kierto Auringon ympäri on paljon muutakin kuin kalenterivuosi. Vuoden mittaan
tapahtuu joukko astronomisesti merkittäviä hetkiä – seisaus- ja tasauspäiviä,
etäisyysvaihteluita ja akselin suunnan vaikutuksia – jotka kaikki yhdessä
muovaavat maapallon ilmastollista ja valollista rytmiä.
Akselin kaltevuus – vuodenaikojen perusta
Maapallon pyörimisakseli on kallistunut noin 23,44 asteen
kulmaan kiertoratansa tasoon nähden. Tämä kallistuma säilyy suunnilleen samana
Maan kiertäessä Auringon ympäri. Tämän seurauksena eri vuodenaikoina Auringon
säteet osuvat eri alueille eri kulmassa ja eri korkeudelta, mikä aiheuttaa
vuodenajat. Ilman tätä kallistumaa ei olisi talvea, kesää eikä kevättä – vain
tasainen, trooppinen ilmasto lähes koko planeetalla.
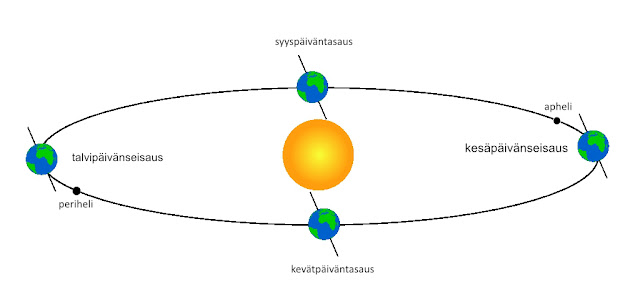
Maapallon vuodessa on astronomisesti muutama mielenkiintoinen piste. Kuva © Kari A. Kuure.
Tasauspäivät – kun valo ja pimeä lähes tasapainossa
Kevätpäiväntasaus (noin [1] 20. maaliskuuta) ja
syyspäiväntasaus (noin 22.–23. syyskuuta) ovat hetkiä, jolloin Aurinko paistaa
suoraan päiväntasaajalle. Usein sanotaan, että tällöin päivä ja yö ovat yhtä
pitkät kaikkialla, mutta todellisuudessa tämä ei pidä tarkasti paikkaansa.
Ilmakehä taivuttaa auringonvaloa siten, että Aurinko näkyy
vielä vähän sen jälkeen, kun se on geometrian mukaan horisontin alapuolella.
Lisäksi Auringolla on halkaisijaa – sen yläreuna nousee ja laskee eri aikaan
kuin keskikohta. Näin ollen päivä on tasauspäivinä yleensä 6–10 minuuttia
pidempi kuin yö, riippuen havaintopaikasta.
Napapiirien läheisyydessä tasauspäivien merkitys liittyy
ennen kaikkea siihen, milloin Aurinko alkaa jälleen nousta pitkän kaamoksen
jälkeen tai milloin se laskee viimeisen kerran ennen yötöntä yötä.
Seisauspäivät – vuoden ääripisteet
Kesäpäivänseisaus (noin 20. – 21. kesäkuuta) on hetki,
jolloin Aurinko on korkeimmillaan pohjoisella taivaalla ja päivä on
pisimmillään. Talvipäivänseisaus (noin 21. – 22. joulukuuta) puolestaan on
vuoden lyhin päivä, jolloin Aurinko käy matalimmillaan.
Napapiirin pohjoispuolella Aurinko ei laske lainkaan kesällä
eikä nouse lainkaan talvella. Tätä kutsutaan yöttömäksi yöksi ja kaamokseksi.
On kuitenkin huomattava, että kaamos ei ala tarkalleen napapiiriltä, vaikka
napapiiri määritelläänkin sen mukaan, missä Aurinko juuri ja juuri ei nouse tai
laske seisauspäivinä. Ilmakehän taite ja Auringon kiekon koko nostavat Auringon
näkyviin vielä hieman geometristen rajojen ulkopuolellakin. Näin ollen
todellinen kaamos alkaa vasta noin 67,4 asteen pohjoisella leveysasteella –
siis esimerkiksi hieman Sodankylän pohjoispuolella.
Maan kiertorata ei ole ympyrä
Maapallon kiertorata ei ole tarkalleen ympyrä, vaan hieman
soikea. Tämän vuoksi Maan etäisyys Auringosta vaihtelee. Maa on lähimpänä
Aurinkoa (perihelissä) noin 3. tammikuuta, jolloin etäisyys on noin 147,1
miljoonaa kilometriä. Kauimpana (aphelissä) Maa on noin 4. heinäkuuta, jolloin
etäisyys on noin 152,1 miljoonaa kilometriä.
Tämä etäisyysero aiheuttaa noin 7 % vaihtelun
säteilytehossa. Vaikka se on havaittava ero, se ei aiheuta vuodenaikoja –
akselin kallistuma on siihen verrattuna paljon merkittävämpi tekijä. Tämä
tietysti jokainen huomaa, sillä heinäkuussa on paljon lämpimämpää kuin
tammikuussa.
Vuodenaikojen kesto ei ole symmetrinen
Vuodenaikojen pituudet eivät ole keskenään yhtä pitkät.
Pohjoisella pallonpuoliskolla kesä kestää hieman pidempään (noin 93 päivää)
kuin talvi (noin 89 päivää). Tämä johtuu Keplerin laeista: Maa liikkuu
radallaan nopeammin ollessaan lähempänä Aurinkoa (perihelissä, eli pohjoisen
talvella) ja hitaammin kauempana (aphelissä, eli pohjoisen kesällä).
Eteläisellä pallonpuoliskolla tilanne on päinvastainen –
siellä kesä on lyhyempi mutta intensiivisempi, koska Aurinko on silloin
lähempänä.

Prekessio muuttaa niin tähtitaivaan koordinaatteja kuin Maan vuoden tapahtumien päivämääriä jos niitä ei korjattaisi tasaisin välein. Kuva © Kari A. Kuure.
Pitkän aikavälin vaihtelut
Maapallon akselin suunta ei pysy täysin muuttumattomana. Se
piirtää hitaasti kartion muotoista liikettä, jota kutsutaan prekessioksi.
Tämä liike kestää noin 26 000 vuotta. Lisäksi akselin kallistuskulma vaihtelee
22,1 ja 24,5 asteen välillä noin 41 000 vuoden jaksoissa, ja kiertoradan muoto
muuttuu vielä pidemmillä aikaskaaloilla.
Näiden kolmen mekanismin – prekession, akselikulman
muutoksen ja radan soikeuden – yhdistelmä muodostaa niin kutsutut Milankovićin
syklit. Niiden uskotaan vaikuttavan maapallon pitkän aikavälin ilmastollisiin
vaihteluihin, kuten jääkausien rytmiin.
Suomen näkökulma – valon vuoristorata
Suomen leveysasteilla päivän pituuden vaihtelu vuoden aikana
on dramaattista. Esimerkiksi Helsingissä päivän pituus vaihtelee noin 6
tunnista yli 18 tuntiin. Pohjoisessa – vaikkapa Utsjoella – vaihtelu on vielä
suurempaa: kesällä Aurinko ei laske lainkaan moneen viikkoon, talvella taas ei
nouse viikkoihin.
Kaamos ei kuitenkaan ulotu napapiirille asti, vaikka se
olisi looginen raja. Ilmakehän taite ja Auringon kiekon koko siirtävät
todellista pimeän jakson alkua pohjoisemmaksi. Rovaniemen korkeudella Aurinko
pysyy hyvin matalalla [2] talvipäivänseisauksen aikaan, mutta nousee
silti näkyviin – jos horisontti sen sallii.
Taivaallinen aikakello
Maapallon kiertoliike Auringon ympäri on taivaallinen
aikakello, jonka osoittimina toimivat valo, varjo ja lämpö, sekä joskus
aurinkokello pihamaalla. Seisauspäivät ja tasauspäivät, perihelit ja aphelit
eivät ole vain taulukoidut hetket vaan konkreettisia käännekohtia ajassa ja
luonnon rytmissä. Meidän arkinen aikakäsityksemme on yhä sidoksissa tähän
suureen, säännölliseen kiertoon, vaikka sitä ei ehkä enää aina tule
ajatelleeksi.
|
Tapahtuma |
Päivämäärä (2025) |
Ilmiö |
|
Periheli |
4. tammikuuta |
Maa lähimpänä Aurinkoa |
|
Kevätpäiväntasaus |
20. maaliskuuta |
Aurinko päiväntasaajalla |
|
Kesäpäivänseisaus |
21. kesäkuuta |
Pohjoisen pisin päivä |
|
Apheli |
4. heinäkuuta |
Maa kauimpana Auringosta |
|
Syyspäiväntasaus |
22. syyskuuta |
Aurinko taas päiväntasaajalla |
|
Talvipäivänseisaus |
21. joulukuuta |
Pohjoisen lyhin päivä |
Viitteet
[1] Päiväntasaus- ja seisauspäivien tarkka päivämäärä
vaihtelee muutamasta syystä, jotka liittyvät Maan liikkeeseen ja kaltevuuteen:
Tärkein syy vaihteluun on karkausvuosien järjestelmä. Maan
kierto Auringon ympäri ei ole tasan 365 päivää, vaan noin 365,2422 päivää.
Kalenterimme pyöristää vuoden 365 päivään, ja karkauspäivä 29. helmikuuta
lisätään joka neljäs vuosi tasapainottamaan tätä eroa. Ilman karkauspäiviä
kalenterivuosi ja todellinen aurinkovuosi siirtyisivät vähitellen toisistaan,
jolloin vuodenajat ja niihin liittyvät tapahtumat, kuten tasauspäivät,
osuisivat eri aikoihin kalenterissa.
Myös muiden Aurinkokunnan planeettojen gravitaatio vaikuttaa
hieman Maan kiertorataan ja sen nopeuteen. Nämä pienet vetovoimat voivat
muuttaa Maan rataa hyvin vähän, mikä puolestaan voi siirtää tasauspäivien
ajankohtia. Nämä vaikutukset ovat kuitenkin hyvin pieniä verrattuna
karkausvuosien ja radan elliptisyyden vaikutukseen.
Pitkällä aikavälillä Maan akselin prekessio eli Maan
pyörimisakselin hidas huojunta vaikuttaa tasauspäivien ajankohtaan. Maan
akselin asento muuttuu hitaasti noin 26 000 vuoden syklillä, mikä saa aikaan
sen, että tasaus- ja seisauspäivät siirtyvät vähitellen aikaisemmaksi
gregoriaanisessa kalenterissa. Tämä vaikutus on kuitenkin vuositasolla niin
vähäinen, ettei sitä yleensä huomaa ilman tarkkaa mittausta.
Nämä tekijät yhdessä aiheuttavat sen, että tasaus- ja
seisauspäivien päivämäärät voivat vaihdella hieman vuosittain, yleensä päivällä
tai kahdella. Tästä syystä myös tekstissä käytetään ilmaisua ” noin”.
[2] Auringon ja Kuun nousu- ja laskuajat määritellään
näiden kappaleiden yläreunan mukaan, kun taas päiväntasaukset ja pohjoiset ja
eteläiset deklinaatiot näkyvän kiekon keskipisteen mukaan.





